如何输入数据

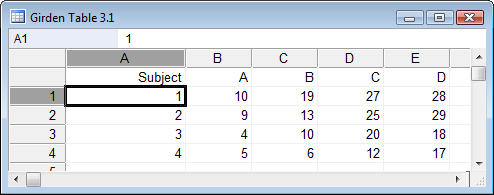
在第一列中，输入每种情况的标识号（不是必需的）。接下来的列包含不同测量的数据（示例取自Girden，1992，表3.1）。

必填项

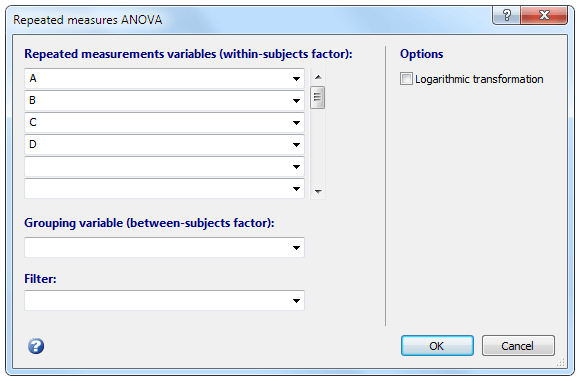
• 重复测量变量：包含不同测量的变量。请注意，选择变量的顺序对于趋势分析很重要。
• 分组变量：未在单因素研究中使用。
• 选择：一个可选过滤器，仅包括案例的选定子组。
• 选项
  对数转换：如果数据需要对数转换（例如，当数据正偏时），请选择对数转换选项。

结果

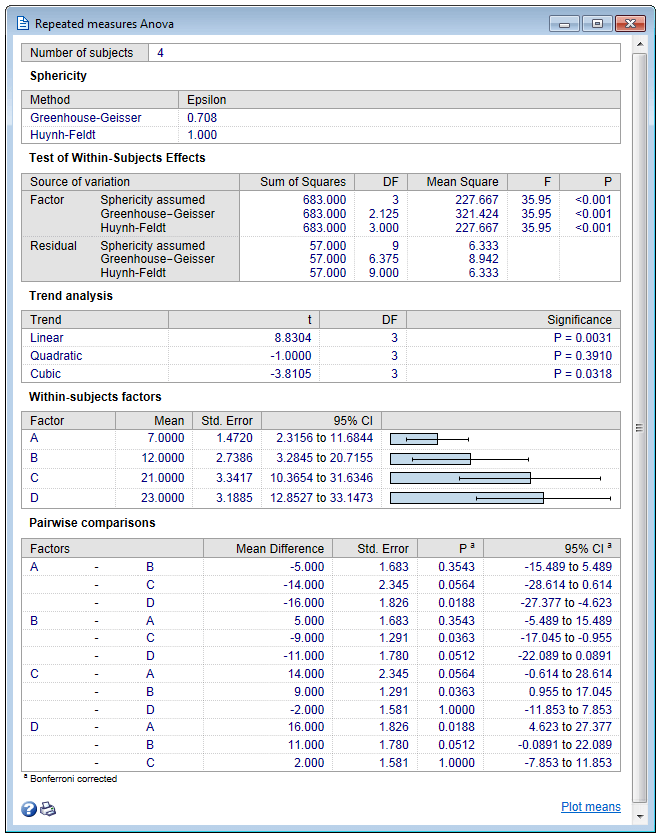
结果窗口显示研究中的主题数。请注意，缺少任何测量值的主题将从分析中删除。

球形度

球形度是指测量之间差异的方差相等，这是具有重复测量因子的ANOVA假设。

MedCalc报告了Greenhouse和Geisser（1958）以及Huynh和Feldt（1976）提出的球形度估计值（ε）（由Lecoutre修正，1991）。epsilon越接近1，差异的方差就越均匀，因此数据越接近球形。Greenhouse-Geisser和Huynh-Feldt估计均用作校正因子，该校正因子应用于自由度，自由度用于计算F观测值的P值。

内科测试

在此表中，显示归因于“因子”和“残差”变体的变体。如果“因子”旁边的P值很低（P <0.05），则可以得出结论，不同测量之间存在显着差异。

MedCalc根据Greenhouse和Geisser（1958）以及Huynh和Feldt（1976）（由Lecoutre，1991校正）的球形度估计值进行两次校正。Girden（1992）建议，当ε（Greenhouse-Geisser估计）> 0.75时，应使用根据Huynh和Feldt进行的校正。如果epsilon <0.75，则首选根据Greenhouse-Geisser进行更保守的校正。

趋势分析

趋势分析表显示测量结果显示线性还是非线性（二次，三次）趋势。

主体内因素

主题内因素汇总在带有平均值，标准误和95％置信区间的表格中。

成对比较

在成对比较表中，将不同的测量结果相互比较。给出了具有标准误差，P值和95％置信区间的平均差异。将多个比较的Bonferroni校正应用于P值和置信区间。

如何输入数据

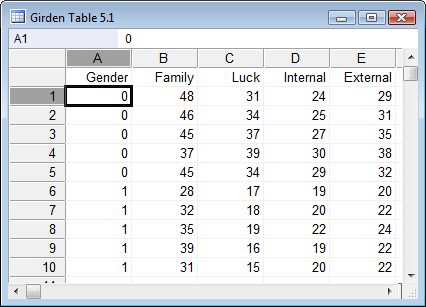
在此示例中，第一列指示组成员身份。“男性”已编码为0，“女性”已编码为1。接下来的列包含不同测量值的数据（示例取自Girden，1992，表5.1）。

必填项

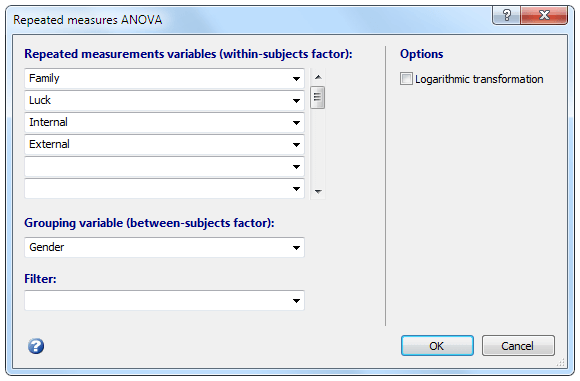
• 重复测量变量：包含不同测量的变量。
• 分组变量：将数据划分为组（对象间因素）的分类变量。
• 选择：一个可选过滤器，仅包括案例的选定子组。
• 选项
  对数转换：如果数据正偏，请选择此选项。

结果

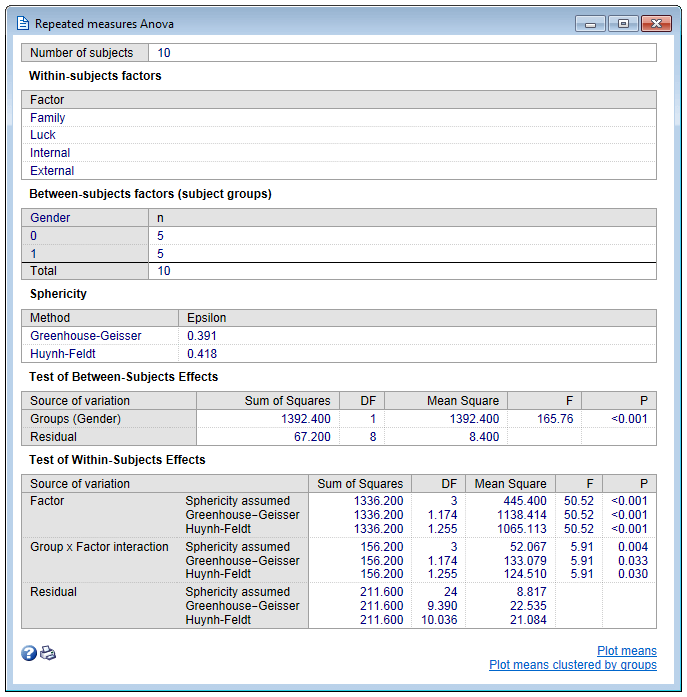
学科间因素（学科组）

第一个表列出了不同的主题组和观察值的数量。

球形度

球形度是指测量之间差异的方差相等，这是具有重复测量因子的ANOVA假设。

MedCalc报告了Greenhouse和Geisser（1958）以及Huynh和Feldt（1976）提出的球形度估计值（ε）（由Lecoutre修正，1991）。epsilon越接近1，差异的方差就越均匀，因此数据越接近球形。Greenhouse-Geisser和Huynh-Feldt估计均用作校正因子，该校正因子应用于自由度，自由度用于计算F观测值的P值。

主体间效应测试

在该表中，显示归因于“组”（对象之间）和“剩余”变量的变量。

• 如果“组”的P值较低（P <0.05），则可以得出结论，各组之间存在显着差异。

主体内效应测试

在此表中，显示了归因于“因子”（对象内），“组”和“因子”交互作用，“剩余”变异的变异源。

• 如果“因子”的P值较低（P <0.05），则可以得出结论，测量之间存在显着差异。
• 如果“组x因子相互作用”的P值较低（P <0.05），则可以得出结论，测量之间的差异取决于组成员。

MedCalc根据Greenhouse和Geisser（1958）以及Huynh和Feldt（1976）（由Lecoutre，1991校正）的球形度估计值进行两次校正。Girden（1992）建议，当ε（Greenhouse-Geisser估计）> 0.75时，应使用根据Huynh和Feldt进行的校正。如果epsilon <0.75，则首选根据Greenhouse-Geisser进行更保守的校正。