命令：	统计 生存分析 Cox比例风险回归

描述

带有对数秩检验的Kaplan-Meier方法可用于比较两组或更多组的生存曲线，而Cox回归（或Cox比例风险模型）可以分析几种风险因素对生存的影响。

终点（死亡或其他任何感兴趣的事件，例如疾病复发）的可能性称为危害。危害建模为：

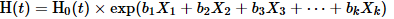
其中X ₁ … X _k是预测变量的集合，而H ₀（t）是时间t的基准危害，代表对于所有预测变量的值为0的人的危害。

通过将上述方程式的两边除以H ₀（t）并取对数，我们得到：

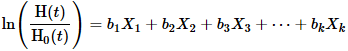
我们将H（t）/ H ₀（t）称为危险比。系数b _i … b _k是通过Cox回归估算的，可以用与多元逻辑回归相似的方式解释。

假设协变量（风险因子）是二分法，如果存在则编码为1，如果不存在则编码为0。然后，假设存在风险因子的个体与没有风险因子的个体相比，假设存在风险因子的个体相对于没有风险因子的个体，则数量exp（b _i）可以随时解释为事件的瞬时相​​对风险。其他协变量。

假设协变量是连续的，则对于任何一个变量，exp（b _i）都是事件在任何时候的瞬时相对风险，与另一个变量相比，协变量值增加了1在所有其他协变量上相同。

必填项

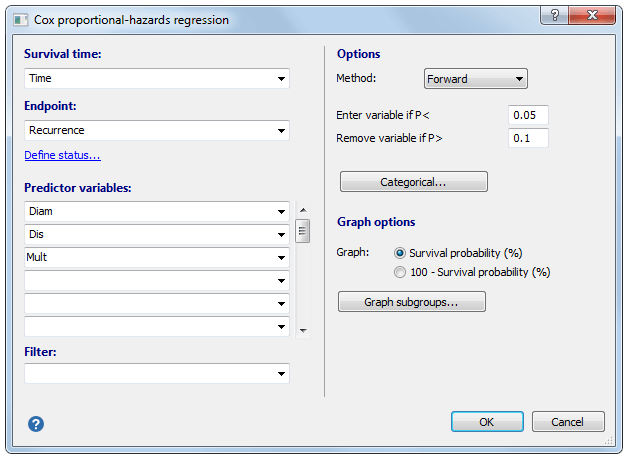
生存时间：变量名称，其中包含达到感兴趣事件的时间或后续时间。

端点：变量的名称，其中包含到达终止点的案例的代码1，或未到达终结点的案例的代码0，因为它们已退出研究或到达研究结束。如果您的数据编码方式不同，则可以使用“定义状态”工具重新编码数据。

预测变量：您希望预测生存时间的变量的名称。

Cox比例回归模型假设预测变量的影响随时间变化是恒定的。此外，端点和预测变量之间应存在线性关系。具有高度偏斜分布的预测变量可能需要对数转换以减少极值的影响。变量var的对数变换可以通过输入LOG（var）作为预测变量来获得。

过滤器：一种过滤器，仅在图中包括个案的选定子组。

选件

• 方法：选择将自变量输入模型的方式。
  • 输入：只需一步即可输入模型中的所有变量，而无需检查
  • 转发：依次输入重要变量
  • 向后：首先将所有变量输入模型，然后依次删除不重要的变量
  • 逐步：依次输入重要变量；在模型中输入变量后，检查并可能删除变得不重要的变量。
• 如果P <
  如果其关联的显着性水平小于此P值，则将变量输入模型中，然后输入变量。
• 如果P>如果
  变量的关联显着性水平大于此P值，则从模型中删除变量，然后删除变量。
• 分类：单击此按钮以标识名义分类变量。

图形选项

• 图形：
  • 生存几率（％）：绘制生存几率（％）与时间的关系（下降曲线）
  • 100-生存几率（％）：绘制100-生存几率（％）随时间变化（上升曲线）
• 图形子组：在这里您可以选择一个预测变量。该图将显示此协变量中所有值的不同生存曲线（必须是分类的，并且最多可以包含8个类别）。如果此处未选择协变量，则该图将显示模型中协变量均值的生存期。

  

结果

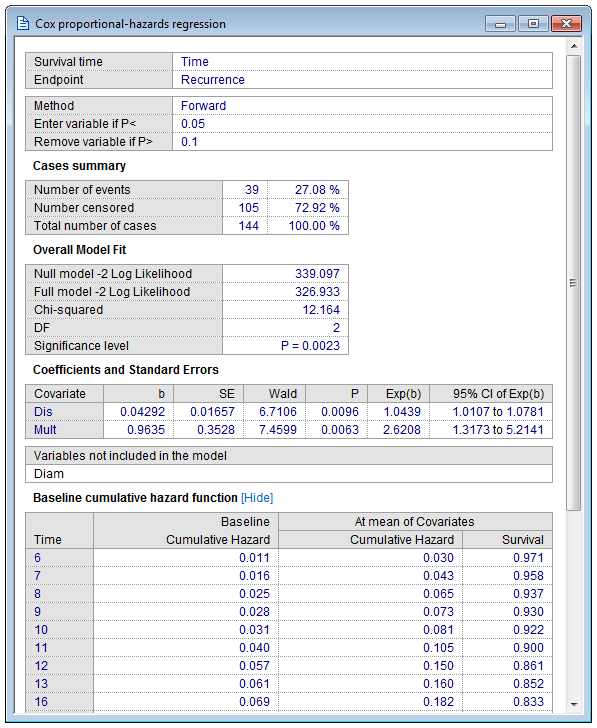
在该示例中（取自Bland，2000年），“存活时间”是胆石溶解后复发的时间（可变时间）。重复发生在变量“重复发生”中（1 =是，0 =否）。预测变量为Dis（=溶解以前的胆结石的月数），Mult（对于多个先前的胆结石为1，对于先前的单个胆结石为0）和Diam（先前的胆结石的最大直径）。

案例总结

该表显示到达终结点的案例数（事件数），未到达终结点的案例数（受检查的数量）以及案例总数。

整体模型拟合

卡方统计量检验时间与模型中所有协变量之间的关系。

系数和标准误差

使用正向选择方法，将两个协变量Dis和Mult输入模型中，这对时间的预测有显着影响（Dis为0.0096，Mult为0.0063 ）。

MedCalc列出了回归系数b，其标准误差，Wald统计量（b / SE）²，P值，Exp（b）和Exp（b）的95％置信区间。

几个月的溶出系数（连续变量Dis）为0.0429。Exp（b）= Exp（0.0429）为1.0439（95％置信区间为1.0107至1.0781），这意味着对于以前的胆结石溶解时间增加1个月，复发的风险比增加1.04倍。在2个月内，危险比增加了1.04 ²倍。

多个胆结石的系数（二分变量Mult）为0.9335。Exp（b）= Exp（0.9635）为2.6208，这意味着先前有胆结石的病例比单块结石的病例更有可能复发2.6208（95％置信区间1.3173至5.2141）。

模型中不包含的变量

发现变量Diam对时间的预测没有显着贡献，并且未包含在模型中。

基准累积危害函数

最后，该程序列出了基准累积危害H ₀（t），其中累积危害和生存率为模型中所有协变量的平均值。

基线累积危害可用于计算在任何情况下在时间t的生存概率S（t）：

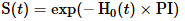
PI是预后指标：

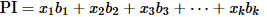
图形

该图显示了分类变量Mult的所有类别的生存曲线（如果有多个先前的胆结石，则为1；如果是单个先前的胆结石，则为0），并显示模型中所有其他协变量的平均值。

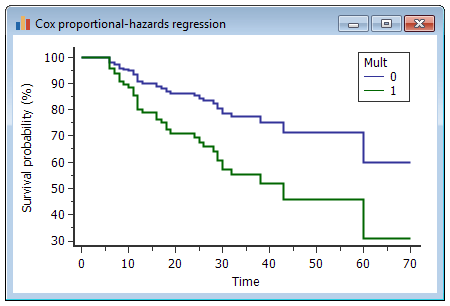
如果没有为“图-子组”选择任何协变量，或者如果模型中未包含所选变量，则该图将在模型中所有协变量的平均值处显示一条生存曲线。

ROC曲线分析

评估Cox比例风险回归模型的另一种方法是利用ROC曲线分析（Harrell等人，1996； Pencina＆D’Agostino，2004）。在此分析中，通过ROC曲线下的面积（AUC）量化了模型的预后指标对阳性和阴性病例的区分能力。的AUC，有时被称为C-统计量（或一致性指数）（勒尔等人，1996），是从0.5改变（区分能力不优于机会）的值到1.0（完美辨别能力）。

样本量注意事项

基于Peduzzi等的工作。（1995年）可以建议以下指南，以将最少病例数纳入研究。

令p为总体中阳性病例（达到终点的病例）和阴性病例（没有达到终点的病例）中最小的比例，k为预测变量的数量，则要包括的最小病例数为：

N = 10 k / p

例如：您有3个预测变量包含在模型中，阳性病例在总体中的比例为0.20（20％）。所需的最少案件数是

N = 10 x 3 / 0.20 = 150

如果结果数小于100，则应按照Long（1997）的建议将其增加到100。