Passing&Bablok(1983)提出了一种适用于方法比较研究的非参数回归分析的统计方法。该过程是对称的,并且在存在一个或几个离群值的情况下具有鲁棒性。但是,它的主要优点可能是(或者更确切地说-似乎)易于解释,这可以解释其在方法比较研究中的广泛使用。
简而言之,Passing-Bablok过程使用非参数方法拟合线性方程y = a + b x的参数a 和b。系数b通过取任意两点之间的直线的所有斜率的中值来计算,其中b = 0或b = ∞的线除外。该参数 一个由下式计算一{Y =中位数我– b X我 }。对于a和b计算出95%的置信区间(CI)。仅当x和y之间存在线性关系时,Passing-Bablok程序才有效,可以通过cusum检验对其进行评估(Passing&Bablok,1983)。
然后将结果解释如下。如果0是在的CI一个,并且1是的CI b,这两种方法是所研究的浓度范围内具有可比性。Passing&Bablok(1983)提出了一个更强的说法:“如果我们同时接受b = 1和a = 0,我们可以推断y * = x *,或者换句话说,这两种方法是相同的”。如果0不在a的CI中 ,则存在系统差异;如果1不在b的CI中, 则两种方法之间存在比例差异。
方程y = a + b x定义了回归线,但并非所有观察值都位于该线上。实际上,观察不是由等式y = a + b x定义的,而是由y = a + b x + e定义的,其中e(残差)是观测到的y值与回归方程预测的值之差对应的x值。Passing&Bablok(1983)建议将残差计算为与拟合线的正交距离。这仅仅是上述残差的线性变换。
残差代表校正系统和比例差异后的剩余变化。
由于该过程假定为线性关系,因此残差应显示为随机模式,并且应接近于正态分布。因此,95%的残差应位于残差标准偏差的±1.96倍的区间内。然后,该间隔定义了两种实验室方法之间的随机差异。
当截距接近于0且斜率接近于1时,残差图与偏差图具有明显的对应关系(Bland&Altman 1986; Krouwer 2008),其解释也可以相似。
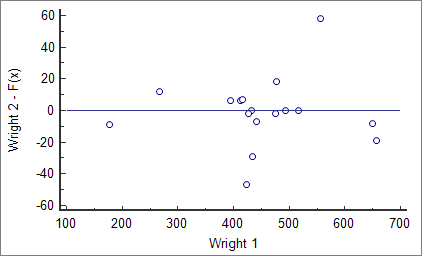
Passing-Bablok回归残差图。数据来自Bland&Altman(1986)。残留标准偏差= 22.46。
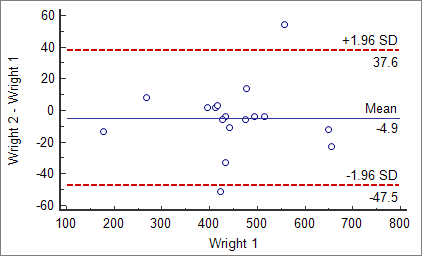
偏差图以协议界线为限。为了与上面的残差图进行比较,针对方法1绘制了差异。
偏差图显示了两种方法之间可以预期的差异,但是哪些差异是可以接受的?
Jensen&Kjelgaard-Hansen(2010)提供了两种方法来定义两种方法之间的可接受差异。在第一方法中,计算这两种方法的组合的固有的不精确性(CV 2方法1 + CV 2方法2)1/2,或者以一式两份测量的情况下[(CV 2方法1 /2)+(CV 2方法2)/ 2)] 1/2。在第二种方法中,接受极限基于分析质量规范,例如临床实验室改进修正案(CLIA)报告的质量标准。第三种方法可能是根据临床要求确定接受限度。如果观察到的随机差异太小而无法影响诊断和治疗,则这些差异可能是可以接受的,并且可以认为两种实验室方法是一致的。
关于样本大小,显而易见的是,当样本大小变小时,CI变大(变宽),并且在截距的CI中出现0,在斜率的CI中出现1的可能性增加。结果是,基于小样本量的方法比较研究倾向于得出实验室方法一致的结论。因此,Passing-Bablok回归的样本量应该不小。Ludbrook(2010)的样本量至少为50。Passing&Bablok(1984)给出了适当样本量的更详细估计。
我们得出结论,Passing&Bablok(1983)“如果我们同时接受b = 1和a = 0,则可以推断y * = x *,或者换句话说,这两种方法是相同的”的说法是错误的,并且两者当残差的置信区间较大时,实验室方法不一致。
我们建议,用于方法比较研究的Passing-Bablok回归分析不应仅限于以95%CI估计截距和斜率。截距是系统差异的度量,斜率是比例差异的度量,残差表示随机差异,应将其包括在统计分析和方法比较报告中。
