| 命令: | 统计 方差分析 方差分析 双向方差分析 双向方差分析 |
描述
方差的双向分析是对方差的单向分析的扩展。一个因变量连续变量Y有两个定性因子(A和B)。
在此过程中测试了三个原假设:
- 因子A不影响变量Y
- 因子B不影响变量Y
- 因子A对变量Y的影响不取决于因子B(即,因子A和B没有相互作用)。
方差的双向分析需要两个定性因子A和B的每种组合都有数据。
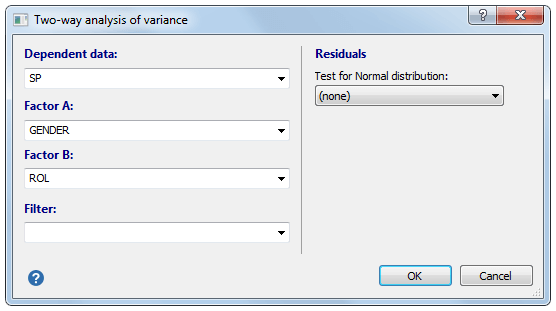
必填项
选择(连续)因变量(Y)和两个离散变量作为可疑影响因变量的定性因子(A和B)。定性因子A和B可以由数字或字母数字数据组成。还可以定义一个过滤器,以便仅包括案例的选定子组。
残差
结果
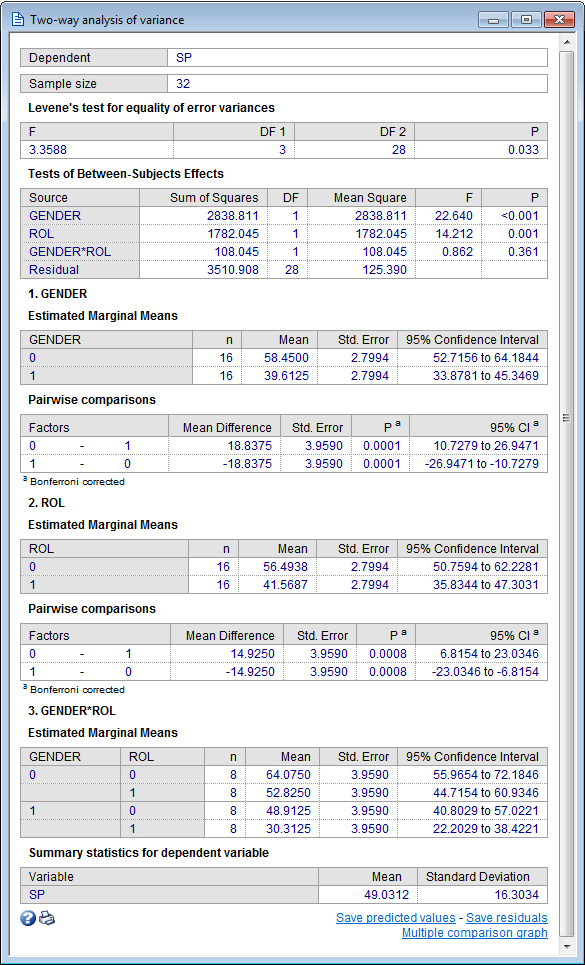
Levene检验方差相等
在ANOVA检验之前,进行Levene方差相等检验。如果Levene检验为阳性(P <0.05),则各组的方差是不同的(各组不是同质的),因此不符合ANOVA的假设。
主体间效应的检验
如果两个主要因子A和B或两个因子相互作用的计算P值小于常规的0.05(5%),则拒绝相应的原假设,并且您接受存在以下假设的替代假设:群体之间确实存在差异。
当2因子相互作用显着时,因子A的作用取决于因子B的水平,因此不建议解释主要因子的均值和均值之间的差异(见下文)。
估计边际均值
在下表中,给出了两个因素所有水平的标准误差和置信区间为95%的平均值。此外,还报告了两组之间的差异,包括标准误差和Bonferroni校正的P值以及差异的95%置信区间。
残差分析
双向ANOVA分析假设残差(观测值与估计值之间的差)服从正态分布。可以通过正式测试或通过图形方法来评估此假设。
当样本量较小时,不同的正态分布正式测试可能没有足够的能力来检测与正态分布的偏差。另一方面,当样本量较大时,由于中心极限定理,正态分布的要求不太严格。
因此,通常优选使用直方图,盒须图或正态图在视觉上评估残差分布的对称性和峰值。
为此,请在结果窗口中单击“保存残差”超链接。这会将残值保存为电子表格中的新变量。然后,您可以在不同的分布图中使用此新变量。
